La geometria definita non euclidea si costruisce su principi che non accettano e negano alcuni postulati di Euclide, nello specifico quelli che riguardano le rette parallele, contenuti nel V postulato.
Riportiamo il concetto espresso dal V postulato di Euclide:
– P1 all’interno di un piano, si afferma che esiste una sola retta che passa attraverso un punto esterno assegnato che risulti parallela ad una retta anch’essa assegnata.
Dal suddetto postulato deriva il teorema che riportiamo:
– T1 la somma degli angoli all’interno di un triangolo è di 180°.
Successivamente, nel 1829 gli studiosi Lobacevskij e Bolyai, di origine ungherese, elaborarono una teoria geometrica che si conferma in linea con quella matematica esposta da Euclide, che esprime quanto segue:
– P2 si afferma che attraverso un punto esterno ad una retta assegnata, sussistono più rette parallele; se si riscontrano più di una retta, significa che ce ne sono una quantità infinita.
Su base di quanto sopra esposto, si deduce quanto segue:
– T2 la somma degli angoli presenti all’interno di un triangolo è inferiore a 180°
Nel corso del 1854 lo studioso Riemann, elaborando le sue teorie in merito alla geometria, espose le sue considerazioni in riferimento ad un possibile ulteriore postulato geometrico che afferma quanto segue:
– P3 attraverso un punto situato all’esterno di una retta assegnata non si riscontra nessuna retta parallela.
Pertanto, per quanto affermato, ne consegue questo teorema:
– T3 la somma degli angoli all’interno di un triangolo è superiore a 180°.
Successivamente, queste tre teorie geometriche sono state puntualizzate dallo studioso Klein, e definte come segue:
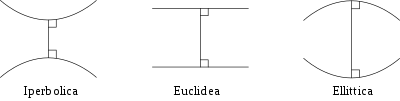
– geometria parabolica
– geometria iperbolica
– geometria ellittica.
Per rappresentare concretamente la differenza di queste teorie dalla geometria euclidea possiamo adoperare alcuni esempi.
Nel caso della geometria ellittica o di Riemann, utilizziamo come riferimento una sfera al posto del piano e convertiamo le forme geometriche proprie del piano nelle forme geometriche equivalenti proprie della superficie sferica.
I punti individuati nel piano equivalgono a punti anche sulla sfera.
Le rette presenti sul piano si traducono nelle circonferenze con il diametro più grande sulla superficie della sfera.
Quindi possiamo affermare che alle rette individuate sul piano equivalgono le linee curve appartenenti alla superfcie della sfera.
Le linee curve possiedono infatti lo stesso carattere distintivo delle linee rette, in quanto rappresentano le linee più corte che uniscono due punti identificati su una superficie.
Quelle che sulla superficie sferica si definiscono geodetiche, rappresentano le circonferenze con il massimo diametro, ovvero le circonferenze risultanti dall’intersezione di un piano che passa al centro della superficie sferica.
Un facile esempio per chiarire il concetto possono essere l’equatore ed i meridiani.
In una sfera non troviamo linee curve che non abbiano punto di incontro, pertanto non abbiamo linee parallele.
Una rappresentazione esemplificative è quella dove si individuano due meridiani in posizione di perpendicolarità rispetto all’equatore e che hanno punto di incontro perpendicolare al polo Nord.
É evidente che in un triangolo delimitato da linee curve ABN troviamo una somma degli angoli interni di 270°.
Pertanto si può affermare che questa tipologia di triangolo presenta una somma degli angoli interni superiore a 180°, ma ciò non è un fattore comune ad ogni triangolo.
Rileviamo quindi che nella teoria geometrica euclidea un triangolo presenta sempre una somma degli angoli interni di 180°, mentre in quella ellittica presenta una somma che varia in funzione dalla dimensione del triangolo.
Altro elemento che caratterizza questa geometria è il rapporto tra la circonferenza ed il raggio che è inferiore alla costante matematica detta π cioè Pi greco.
Ricordiamo infatti che, essendo sulla superficie di una sfera, la circonferenza con diametro AB trova il centro nel punto N e non nel punto C, che invece è un punto situato all’interno della sfera.
Come é chiaro che l’arco denominato AN è più grande del segmento denominato AC, il rapporto tra la circoferenza definita AB e il raggio corrispondente detto AN è inferiore a π.
Realizzare invece un esempio chiaro e funzionale a livello didattico per rappresentare la geometria iperbolica di Lobacevskj risulta più difficile, non esistendo un esempio rappresentativo per questa geometria.
Possiamo immaginare una superficie denominata pseudosfera, proposta come esempio per la geometria iperbolica con curvatura costante in ogni punto, e con forma che ricorda una sella.
Il triangolo formato da curve denominato ABC costruito sulla pseudosfera corrisponde esattamente a un triangolo formato da linee rette sul piano euclideo, perché è composto da linee ricurve, cioè geodetiche.
In questo triangolo la somma degli angoli interni è in funzione della sua grandezza ed è inferiore a 180°.
Possiamo affermare che attraverso il punto denominato P, situato fuori dalla curva R, passano più linee curve dette p1 e p2, che non hanno mai punto di incontro con la curva R, e pertanto ad essa parallele.
Torna alla pagina sulla Geometria.

Alessia T.
Ciao, io sono Alessia e faccio parte del team di Grafica-Facile.com! Ho una grande passione per il design e, avendo molta esperienza nel settore, ho deciso di partecipare in questo bellissimo progetto per condividere il mio sapere sul graphic e web design.
