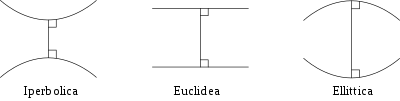
Per comprendere ed apprendere la geometria euclidea è necessario essere a conoscenza di alcuni aspetti basilari, che ci consentiranno di muoverci più agevolmente all’interno della terminologia geometrica.
Innanzi tutto, presentiamo i concetti seguenti e precisamente il concetto primitivo e il concetto di definizione.
Concetto primitivo: si definisce concetto primitivo, un concetto che non ha definizione, poiché visto che è un concetto intuitivo, se ne presuppone chiaramente il suo significato; è possibile che un concetto primitivo sia di tipo geometrico (retta, piano, spazio, punto) o abbia un carattere insiemistico (elemento, insieme, relazione di appartenenza).
Definizione: diversamente dalle definizioni che conosciamo nella lingua italiana, la definizione matematica è univoca, ciò significa che ogni termine possiede uno e solamente un significato.
In aggiunta, ciascuna definizione può contenere solamente termini che siano stati già precedentemente definiti.
Per segnalare gli elementi geometrici vengono usate alcune lettere e precisamente:
- Per i piani lettere greche
- Per i punti lettere maiuscole
- Per le rette lettere minuscole
Dimostrazioni e teoremi
All’interno della geometria euclidea vengono poste alcune affermazioni, che successivamente si giustificano per mezzo di ragionamenti logici.
Queste affermazioni vengono denominate teoremi, e le loro giustificazioni vengono chiamate dimostrazioni.
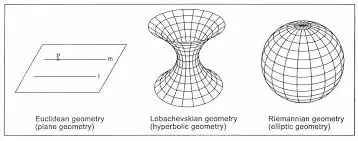
I teoremi generalmente appaiono in questo modo:
- esiste un’implicazione della tipologia A→B (cioè “A implica B “ ), che si definisce enunciato del teorema;
- il primo elemento dell’enunciato ( A ) si definisce ipotesi del problema;
- il secondo elemento dell’enunciato ( B ) si definisce tesi del problema;
- esiste un ragionamento deduttivo, che conduce ad affermare l’attendibilità dell’implicazione, che si definisce come dimostrazione.
- In aggiunta ai teoremi si sente spesso parlare di lemmi e corollari:
Definizione di Lemma: un lemma è un teorema che ha minore importanza e che viene frequentemente usato in una dimostrazione allo scopo di dimostrare il teorema di maggiore importanza.
Definizione di Corollario: il corollario costituisce una immediata conseguenza di un teorema che è stato dimostrato in precedenza.
Al contrario, i postulati costituiscono delle affermazioni che riguardano enti primitivi e che sono accettate come vere, per questo motivo non hanno necessità di una dimostrazione.
Postulati d’ordine
Postulato 4: Si può stabilire una relazione di totale ordine fra i punti di una retta, cioè praticamente è possibile ordinare i punti di una retta facendo in modo che:
- Se vengono dati due punti A e B della retta: o B precede A o A precede B, o A e B coincidono, (proprietà di tricotomia);
- Se A precede B e B precede C, allora è evidente che A precede C (proprietà transitiva).
- Una retta su cui è stato stabilito un verso di percorrenza viene denominata retta orientata.
Postulato 5: Su di una retta orientata ogni punto viene seguito da un altro punto almeno e viene preceduto da un altro punto almeno.
Postulato 6: Fra due punti di una retta viene compreso un terzo punto almeno.
Teorema: Per un punto passa un numero infinito di rette.
L’insieme di tutte le rette, che passano per un medesimo punto, è detto fascio di rette, oppure fascio proprio di rette; viene denominato centro del fascio esattamente il punto comune a tutte le rette.
Al contrario, un fascio improprio di rette si costituisce partendo da una retta e da tutte le rette che le sono parallele.
Postulati di appartenenza
Postulato 0: l’insieme di tutti i punti costituisce lo spazio; piani e rette costituiscono sottoinsiemi dello spazio. Una retta contiene un infinito numero punti, un piano contiene un infinito numero di rette, uno spazio contiene un numero infinito di piani.
Postulato 1: Per due distinti può passare una e solamente una retta.
Il postulato 1 ha una fondamentale conseguenza per cui due distinte rette non hanno la possibilità di avere in comune più di un punto; di conseguenza se abbiamo due rette s e r, queste possono essere:
- incidenti se possiedono un punto in comune; in tal caso si afferma che le rette hanno un’intersezione in quel punto, e il punto viene denominato punto di intersezione;
- non incidenti se non possiedono punti in comune, dunque se non hanno un punto di intersezione.
- I punti si dicono allineati, se fanno parte di una medesima retta.
Due rette giacenti sul medesimo piano e che non hanno mai un punto di intersezione, vengono chiamate parallele.
Postulato 2: Per tre punti che non sono allineati passa uno e solamente un piano.
I punti appartenenti ad un medesimo piano vengono denominati complanari.
Postulato 3: Se due punti di una retta sono appartenenti ad un piano, di conseguenza tutti i punti della retta sono appartenenti a quel piano (la retta è appartenente al piano).
Torna alla pagina sulla Geometria.

Alessia T.
Ciao, io sono Alessia e faccio parte del team di Grafica-Facile.com! Ho una grande passione per il design e, avendo molta esperienza nel settore, ho deciso di partecipare in questo bellissimo progetto per condividere il mio sapere sul graphic e web design.
