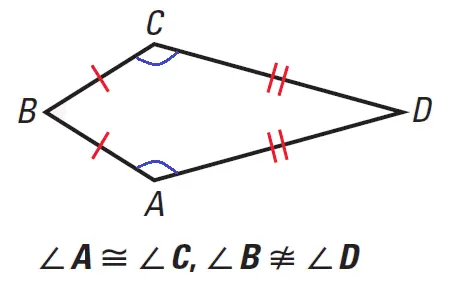
In geometria si definisce deltoide (o aquilone), un quadrilatero in cui compaiono 2 coppie di lati consecutivi congruenti, ossia congruenti a due a due.
Le diagonali, di conseguenza, risultano perpendicolari tra loro.
Se la diagonale minore porta il deltoide a dividersi in due triangoli isosceli, la diagonale maggiore, oltre a dividere la minore in 2 parti congruenti, costituisce la bisettrice degli angoli nati dai lati congruenti.
Dividendo il deltoide in 2 triangoli congruenti, la diagonale maggiore rappresenta anche l’asse di simmetria.
Considerando gli angoli interni, questi non possono essere uguali se questi risultano compresi tra lati congruenti; lo sono, invece, quelli compresi fra i lati “NON” congruenti.
Deltoide concavo e convesso: le differenze
Un deltoide può essere sia concavo o convesso.
Nel primo caso a caratterizzarlo è la presenza, tra gli angoli interni, di un angolo concavo (quindi contenente i prolungamenti di 2 lati).
Nel secondo, invece, convessi sono tutti gli angoli interni; ed è questo a escludere la presenza di prolungamenti dei lati.
La forma assunta da tale tipologia di deltoide l’ha portata ad assumere il nome di “aquilone”.
Le proprietà principali del deltoide
È giunto il momento di indicare le proprietà di questa figura geometrica.
La prima che desidero ricordare è l’esistenza di una coppia di angoli opposti congruenti.
Per poter essere considerato un deltoide, un quadrilatero deve essere in possesso di diagonali perpendicolari; una delle due diagonali, inoltre, è divisa in segmenti congruenti dal loro punto di intersezione.
Il rombo, ad esempio, costituisce un deltoide in cui i 4 lati sono congruenti.
La somma risultante dagli angoli interni di un deltoide è pari a 360°, ossia a un angolo giro.
Ulteriori proprietà del deltoide
Le proprietà che mi appresto a descrivere assumono valore solo per una delle due tipologie principali di deltoide (concava o convessa).
In un deltoide concavo le diagonali non hanno punti di intersezione.
Sempre parlando di diagonali, quelle di un deltoide convesso sono perpendicolari tra loro, ma non solo; infatti si intersecano in un punto interno al deltoide.
Cosa accade a una diagonale di un deltoide convesso che unisce i vertici dei 2 angoli non congruenti?
Assume il ruolo di asse di simmetria, e divide la figura in 2 triangoli congruenti.
Quando si è in presenza 2 angoli congruenti, la diagonale che ne unisce i vertici viene a sua volta divisa in 2 segmenti congruenti dall’altra diagonale.
Allo stesso tempo divide il deltoide in due triangoli isosceli.
Continuando a trattare i deltoidi convessi, voglio sottolineare come le due diagonali diano luogo a 4 triangoli rettangoli.
A costituire le ipotenuse sono i lati del deltoide.
Qualunque deltoide convesso include al suo interno una circonferenza, tangente in tutti i lati; in altre parole, questa tipologia di deltoide è circoscrivibile in ogni caso a una circonferenza.
Il calcolo dell’area del deltoide
Come calcolare l’area di un deltoide sulla base di quanto ho scritto finora?
Per essere considerato tale, un quadrilatero deve avere lati consecutivi congruenti e diagonali perpendicolari.
È possibile così applicare anche in questo caso le formule utilizzate per determinare l’area del rombo: A=(d1xd2)/2, dove la lettera “A” rappresenta l’Area, “d1” la diagonale maggiore e “d2” quella minore.
L’area, quindi, è il risultato ottenuto moltiplicando la misura della diagonale maggiore per quella della diagonale minore, e dividendo il prodotto per due.
Partendo da tale formula, ovviamente, è possibile ricavare le formule inverse.
Pertanto, la diagonale minore è il risultato della formula d=2xA:D, mentre la diagonale maggiore è pari a D=2xA:d
Come determinare il perimetro del deltoide
Ora che ho indicato come ricavare l’area del deltoide, è giunto il momento di parlare del perimetro.
Ottenerlo è altrettanto semplice, in quanto il perimetro di questa figura geometrica si calcola esattamente come quello di rettangolo e romboide.
Le formule utilizzabili sono due.
La prima si basa sulla somma delle due diagonali maggiori e di quelle minori moltiplicata per due.
La seconda è il valore determinato moltiplicando la diagonale maggiore per due e sommando quanto ottenuto alla diagonale minore, moltiplicata anch’essa per due.
Un esempio renderà più chiaro il concetto.
Supponiamo di avere a che fare con un lato di 48 cm, e un secondo lato pari ai suoi 2/5 (quindi di 19,2 cm).
Ricordando nuovamente che la figura presenta 2 coppie di lati consecutivi congruenti, occorrerà sommare: 48+48+19,2+19,2, ottenendo il risultato di 134,40 cm.
Clicca qui per imparare altri concetti di geometria.

Alessia T.
Ciao, io sono Alessia e faccio parte del team di Grafica-Facile.com! Ho una grande passione per il design e, avendo molta esperienza nel settore, ho deciso di partecipare in questo bellissimo progetto per condividere il mio sapere sul graphic e web design.
